Tokamak GOLEM Basic diagnostics

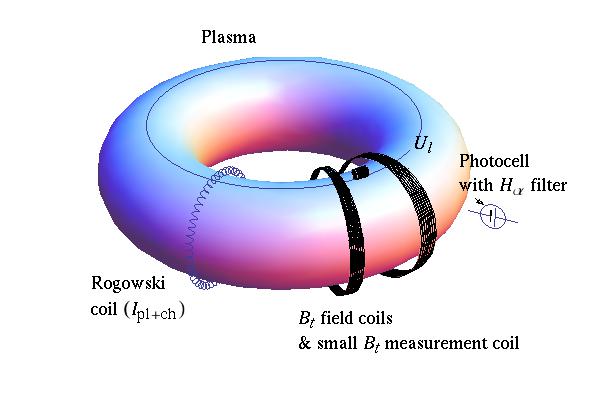
Procedure (This notebook to download)

bash wrapper, Error log

Prerequisities: function definitions

Load libraries

In [1]:
%matplotlib inline
import os
import numpy as np
import matplotlib.pyplot as plt
from scipy import constants, integrate, signal, interpolate
import sqlalchemy   # high-level library for SQL in Python
import pandas as pd

For interactive web figures

In [2]:
import holoviews as hv
hv.extension('bokeh')
import hvplot.pandas

For conditional rich-text boxes

In [3]:
from IPython.display import Markdown

Define global constants.

In [4]:
base_URL = "http://golem.fjfi.cvut.cz/utils/data/{shot_no}/{identifier}" #remote access
data_URL = "http://golem.fjfi.cvut.cz/shots/{shot_no}/DASs/StandardDAS/{identifier}.csv"  # TODO workaround
parameters_URL = 'http://golem.fjfi.cvut.cz/shots/{shot_no}/Production/Parameters/{identifier}'

destination=''
#os.makedirs(destination, exist_ok=True );
# try to get thot number form SHOT_NO envirnoment variable, otherwise use the specified one
shot_no = os.environ.get('SHOT_NO', 0)

The DataSource downloads and caches data (by full URL) in a temporary directory and makes them accessible as files.

In [5]:
ds = np.DataSource(destpath='/tmp')
In [6]:
def print_and_save(phys_quant, value, format_str='%.3f'):
    print(phys_quant+" = %.5f" % value)
    with open(destination+phys_quant, 'w') as f:
        f.write(format_str % value)
    update_db_current_shot(phys_quant,value)    
        
def update_db_current_shot(field_name, value):
    try:
        engine = sqlalchemy.create_engine('postgresql://golem:rabijosille@192.168.2.116/golem_database')
    except:
        return
    engine.execute(f"""UPDATE shots SET "{field_name}"={value} WHERE shot_no IN(SELECT max(shot_no) FROM shots)""")  
    
    
def open_remote(shot_no, identifier, url_template=base_URL):
    return ds.open(url_template.format(shot_no=shot_no, identifier=identifier))

def read_value(shot_no, identifier):
    """Return the value for given shot as a number if possible"""
    value = open_remote(shot_no, identifier, base_URL).read()
    return pd.to_numeric(value, errors='ignore')

def read_parameter(shot_no, identifier):
    return open_remote(shot_no, identifier, parameters_URL).read().strip()
    
def read_signal(shot_no, identifier): 
    file = open_remote(shot_no, identifier, data_URL)
    return pd.read_csv(file, names=['Time',identifier],
                     index_col='Time', squeeze=True)  # squeeze makes simple 1-column signals a Series
In [7]:
def correct_inf(signal):
    """Inteprolate Inf values"""
    signal = signal.replace([-np.inf, np.inf], np.nan).interpolate()
    return signal
In [8]:
t_Bt = float(read_parameter(shot_no, 'TBt')) * 1e-6  # from us to s
t_CD = float(read_parameter(shot_no, 'Tcd')) * 1e-6  # from us to s
offset_sl = slice(None, min(t_Bt, t_CD) - 1e-4)

$U_l$ management

Check the data availability

In [9]:
loop_voltage = read_signal(shot_no, 'LoopVoltageCoil_raw')
polarity_CD = read_parameter(shot_no, 'CD_orientation')
if polarity_CD != 'CW':                   # TODO hardcoded for now!
    loop_voltage *= -1  # make positive
loop_voltage = correct_inf(loop_voltage)
loop_voltage.loc[:t_CD] = 0
ax = loop_voltage.plot(grid=True)
ax.set(xlabel="Time [s]", ylabel="$U_l$ [V]", title="Loop voltage $U_l$ #{}".format(shot_no));

$B_t$ calculation

Check the data availability

It is as magnetic measurement, so the raw data only give $\frac{dB_t}{dt}$

In [10]:
dBt = read_signal(shot_no,'BtCoil_raw')
polarity_Bt = read_parameter(shot_no, 'Bt_orientation')
if polarity_Bt != 'CW':                   # TODO hardcoded for now!
    dBt *= -1  # make positive
dBt = correct_inf(dBt)
dBt -= dBt.loc[offset_sl].mean()
ax = dBt.plot(grid=True)
ax.set(xlabel="Time [s]", ylabel="$dU_{B_t}/dt$ [V]", title="BtCoil_raw signal #{}".format(shot_no));

Integration (it is a magnetic diagnostic) & calibration

In [11]:
K_BtCoil = read_value(shot_no, 'K_BtCoil') # Get BtCoil calibration factor
print('BtCoil calibration factor K_BtCoil={} T/(Vs)'.format(K_BtCoil))

BtCoil calibration factor K_BtCoil=70.42 T/(Vs)
In [12]:
Bt = pd.Series(integrate.cumtrapz(dBt, x=dBt.index, initial=0) * K_BtCoil, 
               index=dBt.index, name='Bt')
ax = Bt.plot(grid=True)
ax.set(xlabel="Time [s]", ylabel="$B_t$ [T]", title="Toroidal magnetic field $B_t$ #{}".format(shot_no));

Plasma + Chamber current $I_{p+ch}$ calculation

Check the data availability

Because it is a magnetic measurement, the raw data only gives $\frac{dI_{p+ch}}{dt}$

In [13]:
dIpch = read_signal(shot_no, 'RogowskiCoil_raw')
if polarity_CD == 'CW':                   # TODO hardcoded for now!
    dIpch *= -1  # make positive
dIpch = correct_inf(dIpch)
dIpch -= dIpch.loc[offset_sl].mean() # subtract offset
dIpch.loc[:t_CD] = 0
ax = dIpch.plot(grid=True)
ax.set(xlabel="Time [s]", ylabel="$dU_{I_{p+ch}}/dt$ [V]", title="RogowskiCoil_raw signal #{}".format(shot_no));

Integration (it is a magnetic diagnostics) & calibration

In [14]:
K_RogowskiCoil = read_value(shot_no, 'K_RogowskiCoil') # Get RogowskiCoil calibration factor
print('RogowskiCoil calibration factor K_RogowskiCoil={} A/(Vs)'.format(K_RogowskiCoil))

RogowskiCoil calibration factor K_RogowskiCoil=5300000.0 A/(Vs)
In [15]:
Ipch = pd.Series(integrate.cumtrapz(dIpch, x=dIpch.index, initial=0) * K_RogowskiCoil,
                index=dIpch.index, name='Ipch')
ax = Ipch.plot(grid=True)
ax.set(xlabel="Time [s]", ylabel="$I_{p+ch}$ [A]", title="Total (plasma+chamber) current $I_{{p+ch}}$ #{}".format(shot_no));

Plasma current $I_{p}$ calculation

In [16]:
R_chamber = read_value(shot_no, 'R_chamber') # Get Chamber resistivity
print('Chamber resistivity R_chamber={} Ohm'.format(R_chamber))

Chamber resistivity R_chamber=0.0097 Ohm
In [17]:
L_chamber = 1e-6  # H

The chamber current $I_{ch}$ satisfies the equation (neglecting the mutual inductance with the plasma) $$U_l = R_{ch} I_{ch} + L_{ch} \frac{d I_{ch}}{dt}$$ Therefore, the following initial value problem must be solved to take into account the chamber inductance properly $$\frac{d I_{ch}}{dt} = \frac{1}{L_{ch}}\left( U_l - R_{ch} I_{ch}\right), \quad I_{ch}(t=0)=0$$

In [18]:
U_l_func = interpolate.interp1d(loop_voltage.index, loop_voltage)  # 1D interpolator
def dIch_dt(t, Ich):
    return (U_l_func(t) - R_chamber * Ich) / L_chamber
t_span = loop_voltage.index[[0, -1]]
solution = integrate.solve_ivp(dIch_dt, t_span, [0], t_eval=loop_voltage.index, )
Ich = pd.Series(solution.y[0], index=loop_voltage.index, name='Ich')
In [19]:
Ip_naive = Ipch - loop_voltage/R_chamber  # creates a new Series
Ip = Ipch - Ich
Ip.name = 'Ip'
Ip_naive.plot(grid=True, label='naive $I_{ch}=U_l/R_{ch}$')
ax = Ip.plot(grid=True, label=r'using $U_l = R_{ch} I_{ch} - L_{ch} \frac{d I_{ch}}{dt}$')
ax.legend()
ax.set(xlabel="Time [s]", ylabel="$I_{p}$ [A]", title="Plasma current $I_{{p}}$ #{}".format(shot_no));
In [20]:
for I in [Ich.rename('$I_{ch}$'), Ipch.rename('$I_{ch}+I_p$'), Ip.rename('$I_p$')]:
    ax = I.plot()
ax.legend()
ax.set(xlabel='Time [s]', ylabel='$I$ [A]', title='estimated plasma and chamber current and measured total')
plt.grid()

Plasma detect

The plasma detection is based on finding the time points of the greatest peaks in the first (smooth) derivative of $I_p$ which corresponds to the breaks in slope of $I_p$, i.e. the rise or fall to 0, respectively. The smooth derivative is found using the Savitzky-Golay filter.

In [21]:
Ip_detect = Ip.loc[0.0025:]  # select time > 2.5 ms to avoid thyristors
dt = (Ip_detect.index[-1] - Ip_detect.index[0]) / (Ip_detect.index.size)  # estimated sampling step
print('Sampling step {dt:.3g} s, sampling frequency {fs:.3g} Hz'.format(dt=dt, fs=1/dt))
window_length = int(0.5e-3/dt)  # window fit over 1 ms
if window_length % 2 == 0:  # must not be odd
    window_length += 1
dIp = pd.Series(signal.savgol_filter(Ip_detect, window_length, polyorder=3, deriv=1, delta=dt),
                name='dIp', index=Ip_detect.index) / 1e6 # [MA/s]

threshold = 0.05
plasma_start = dIp[dIp > dIp.max()*threshold].index[0]   # plasma actually starts before the sharpest rise
plasma_end = dIp.idxmin()  # due to inductance smoothing the greatest fall is the best predictor
is_plasma = int(plasma_start < plasma_end and dIp.abs().max() > 0.5)
print_and_save("b_discharge", is_plasma, "%.3f")
if not is_plasma:
    plasma_start = plasma_end = np.nan
    plasma_lifetime = 0
    print_and_save("t_plasma_start", -1, "%.3f")
    print_and_save("t_plasma_end", -1, "%.3f")
    print_and_save("t_discharge_duration", -1, "%.3f")
else:
    plasma_lifetime = plasma_end - plasma_start
    print_and_save("t_plasma_start", plasma_start*1000, "%.3f")
    print_and_save("t_plasma_end", plasma_end*1000, "%.3f")
    print_and_save("t_discharge_duration", plasma_lifetime*1000, "%.3f")

Sampling step 1e-06 s, sampling frequency 1e+06 Hz
b_discharge = 0.00000
t_plasma_start = -1.00000
t_plasma_end = -1.00000
t_discharge_duration = -1.00000
In [22]:
fig, axs = plt.subplots(3, 1, sharex=True, dpi=200)
dIp.plot(grid=True, ax=axs[0])
axs[0].set(xlabel='', ylabel='$dI_p/dt$ [MA/s]', title='Plasma detection from $d I_p/dt$ in #{}'.format(shot_no))
Ip.plot(grid=True, ax=axs[1])
axs[1].set(ylabel="$I_{p}$ [A]")
loop_voltage.plot(grid=True, ax=axs[2])
axs[2].set(xlabel="Time [s]", ylabel="$U_{l}$ [V]")

for ax in axs:
    for t in (plasma_start, plasma_end):
        ax.axvline(t, color='k', linestyle='--', linewidth=2)
        
plt.savefig('icon-fig')

Overview graphs and parameters

For convenience time is saved and displayed in ms, currents in kA.

In [23]:
df_processed = pd.concat(
    [loop_voltage.rename('U_loop'), Bt, Ip*1e-3, Ich*1e-3], axis='columns')
df_processed.index = df_processed.index * 1e3  # to ms
df_processed.head()
Out[23]:
U_loop Bt Ip Ich
Time
-0.719394 0.0 0.000000e+00 0.0 0.0
-0.718394 0.0 4.037366e-08 0.0 0.0
-0.717394 0.0 7.001927e-08 0.0 0.0
-0.716394 0.0 8.893683e-08 0.0 0.0
-0.715394 0.0 1.135760e-07 0.0 0.0
In [24]:
if is_plasma:
    plasma_lines = hv.VLine(plasma_start*1e3) * hv.VLine(plasma_end*1e3)
else:
    plasma_lines = hv.Curve([])
layout = df_processed['U_loop'].hvplot.line(ylabel='Uâ‚— [V]', xlabel='') * plasma_lines +\
df_processed['Bt'].hvplot.line(ylabel='Bₜ [T]', xlabel='') * plasma_lines +\
df_processed['Ich'].hvplot.line(label='Iᴄʜ') * df_processed['Ip'].hvplot.line(ylabel='Iᴄʜ, Iₚ [kA]', label='Iₚ', xlabel='time [ms]') *\
   plasma_lines

plot = layout.cols(1).opts(
    hv.opts.Curve(width=600, height=200, title='', ylim=(0, None), show_grid=True),
    hv.opts.VLine(color='black', alpha=0.7, line_dash='dashed')
                        )
hvplot.save(plot, 'homepage_figure.html')
plot
Out[24]:
In [25]:
fname = 'basig_diagnostics_processed.csv'
In [26]:
df_processed.to_csv(fname)
In [27]:
Markdown("[Time series in graph in CSV format](./{})".format(fname))
Out[27]:

Time series in graph in CSV format

In [28]:
units = ['V', 'T', 'kA', 'kA']
In [29]:
plasma_start_ms = plasma_start *1e3
plasma_end_ms = plasma_end *1e3
plasma_lifetime_ms = plasma_lifetime * 1e3
In [30]:
if is_plasma:
    heading = Markdown("### Basic diagnostics values during plasma\n\n"
                       "plasma lifetime of {:.3g} ms, from {:.3g} ms to {:.3g} ms".format(
                          plasma_lifetime_ms, plasma_start_ms, plasma_end_ms))
else:
    heading = Markdown("### No plasma detected (vacuum discharge)")
heading
Out[30]:

No plasma detected (vacuum discharge)

In [31]:
if is_plasma:
    plasma_sl = slice(plasma_start_ms, plasma_end_ms)
else:
    plasma_sl = slice(0)   # TODO really use whole discharge ?
df_during_plasma = df_processed.loc[plasma_sl]
df_overview = df_during_plasma.quantile([0.01, 0.5, 0.99])  # use quantiles to skip peaks
df_overview.index = ['min', 'mean', 'max']  # actually quantiles, but easier to understand
if is_plasma:
    df_overview.loc['start'] = df_during_plasma.iloc[0]
    df_overview.loc['end'] = df_during_plasma.iloc[-1]
else:
    df_overview.loc['start'] = df_overview.loc['end'] = np.nan
df_overview.loc['units'] = units
# make units row first
df_overview = df_overview.iloc[np.roll(np.arange(df_overview.shape[0]), 1)]
In [32]:
df_overview
Out[32]:
U_loop Bt Ip Ich
units V T kA kA
min 0 -1.68673e-06 0 0
mean 0 -2.85265e-07 0 0
max 0 8.74426e-07 0 0
start NaN NaN NaN NaN
end NaN NaN NaN NaN
In [33]:
for agg in ('mean', 'max'):
    for quantity, value in df_overview.loc[agg].iteritems():
        print_and_save(quantity+'_'+agg, value)

U_loop_mean = 0.00000
Bt_mean = -0.00000
Ip_mean = 0.00000
Ich_mean = 0.00000
U_loop_max = 0.00000
Bt_max = 0.00000
Ip_max = 0.00000
Ich_max = 0.00000

End of overview row