Numerický model pro vakuový výboj¶
V první části numerického modelu se budeme obdobně jako u table-top experimentu zabývat zjednodušenou verzí výboje v tokamaku a to tzv. Vakuovým výbojem. Nejdříve se ale seznámíme s původními rovnicemi popisující standartní výboj tokamaku Golem. Elektrické uspořádání standartního výboje tokamaku vypadá následovně:
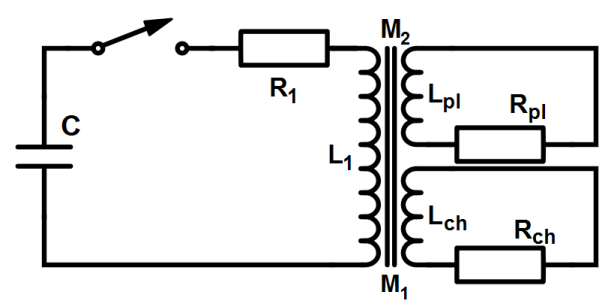
Technické uspořádání je tvořeno jedním primárním a dvěma sekundárními obvody.
Primární obvod tokamaku je tvořen cívkou o indukčnosti $L_1$ (říkáme primární vinutí tokamaku), charakteristickým odporem $R_1$, spínačem a kondenzátorem (v případě tokamaku Golem kondenzátorovou baterií) o kapacitě $C_1$ a nabíjen na hodnotu napětí $U_C$.
První sekundární obvod vyjadřuje indukčnost plazmatu $L_{pl}$ a charakteristickým odporem plazmatu $R_{pl}$. Je nutno podotknout, že plazma je tvořeno pouze jedním závitem na krátko sekundárního vinutí.
Druhý sekundární obvod vyjadřuje indukčnost samotné komory $L_{ch}$ na kterou primární vinutí také působí a odvádí část svojí energie do této komponenty, která má také svůj odpor $R_{ch}$.
Transformátorové jádro spojující tyto všechny vinutí navzájem lze reprezentovat vzájemnou indukčností $M_1$,$M_2$ která díky jejich vzájemné provázanosti je stejná.
Takový systém lze popsat sadou diferenciální tranformátorových rovnic plynoucích z Kirchhoffových zákonů ve tvaru:
\begin{equation} L_1 \frac{d I_1}{dt}+R_1 I_1 + U_C - M_1 \frac{dI_{ch}}{dt} - M_2 \frac{dI_{pl}}{dt}= 0 \end{equation}\begin{equation} M_1 \frac{dI_1}{dt}=R_{ch} I_{ch} + L_{ch} \frac{dI_{ch}}{dt} \end{equation}\begin{equation} M_2 \frac{dI_1}{dt}=R_{pl} I_{pl} + L_{pl} \frac{dI_{pl}}{dt}, \end{equation}kde $I_1$ je proud protékající primárním obvodem s kondenzátorovou baterií, $I_{ch}$ je proud indukovaný na stěnách komory a $I_{pl}$ je proud indukován v plazmatu.
Nutné je však zmínit, že výše uvedený systém zanedbává vzájemné působení komory a plazmatu, které by šlo farakterizovat jejich vzájemnou indukčností a také vliv tyristoru v obvodu v reálném provozu tokamaku, který má taky svoje zastoupení při vývoji samotného výboje.
Vakuový výboj¶
Výše uvedený systém rovnic není uplně triviální vyřešit a ani náš table-top experiment nebude zpočátku uvažovat takto pokročilý systém a proto zde provedeme menší modifikaci, která způsobí značné zjednodušení této soustavy diferenciálních rovnic.
Budeme předpokládat výboj bez plazmatu. Takovou konfiguraci na tokamaku nazýváme tzv. Vakuový výboj, kdy se veškerá indukovaná energie v podobě indukovaného proudu naindukuje pouze na stěně samotné komory.
V tomto duchu proběhla i samotná konstrukce table-top experimentu, protože "veškerá" energie se naindukovala na měděném kroužku obdobně jako v tomto modelu v případě přímé indukce do komory tokamaku.
V případě table-top experimentu hovoříme, že měděný prstenec má reprezentovat proud plazmatem, ale to není potíž, protože v tomto modelu proud protékajícím komorou bude reprezentovat v table top experimentu proud plazmatem. Jedná se jen o jiné pojmenování téhož zkoumaného prvku.
Tento model je tedy reprezentován nasledujícím obvodem:
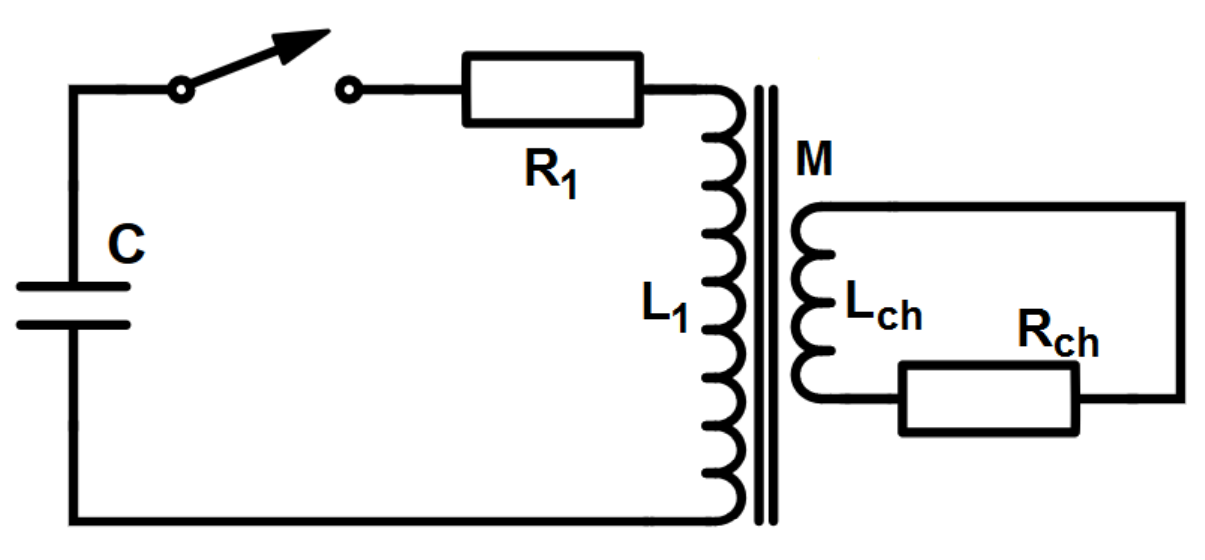
Po tomto zjednodušení dospějeme k následující značně jednodušší soustavě diferenciálních rovnic:
\begin{equation} L_1 \frac{d I_1}{dt}+R_1 I_1 + U_C - M \frac{dI_{ch}}{dt} = 0 \end{equation}\begin{equation} M \frac{dI_1}{dt}=R_{ch} I_{ch} + L_{ch} \frac{dI_{ch}}{dt}. \end{equation}Soustava se nám z původně ze 3 rovnic redukovala a pouhé dvě rovnice a v další sekci se zaměříme na možné vyřešení této soustavy.
Řešení soustavy transformátorových rovnic pro Vakuový výboj¶
V prvním kroku danou soustavu upravíme pomocí definice proudu jako změny příslušného protékajícího náboje za čas. V primární obvodu označíme protékaný náboj $Q$ a náboj protékající sekundárním obvodem označíme jako $q$.
Podle definice zavedeme napětí na kondenzátoru jako $U_C=\frac{Q}{C}$, proud primárním obvodem jako $I_1=\frac{dQ}{dt}$ a proud sekundárním obvodem jako $I_{ch}=\frac{dq}{dt}$. Po dosazení příslušných výrazů do soustavy se nám soustava značně změní do tvaru:
\begin{equation} \frac{d^2 Q}{dt^2} - \frac{M}{L_1} \frac{d^2 q}{dt^2} + \frac{R_1}{L_1} \frac{dQ}{dt} + \frac{Q}{L_1 C} = 0 \end{equation}\begin{equation} \frac{d^2 Q}{dt^2} - \frac{L_{ch}}{M} \frac{d^2 q}{dt^2} + \frac{R_{ch}}{M} \frac{dq}{dt} = 0. \end{equation}Ze soustavy diferenciálních rovnic je patrné, že jsme předchozím krokem soustavu převedli ze soustavy dvou diferenciálních rovnic prvního řádu na dvě diferenciální rovnice druhého řádu s neznámými funkcemi $Q(t)$ a $q(t)$, které jsou těmito neznámými funkcemi navzájem provázány, což budeme muset v dalších krocích vyřešit, protože tuto soustavu nelze řešit přímo. Protože se jedná o soustavu dvou diferenciálních rovnic s dvěma neznámými funkcemi, tak budeme potřebovat pro nalezení konkrétního řešení rovnou čtyři počáteční podmínky.
Počáteční podmínky pro neznámou funkci $Q(t)$ v primárním obvodu tvoří $Q(0)=C\cdot U_C$ a $Q'(0) = I_1(0) = 0$. V případě sekundárního obvodu pro neznámou funkci $q(t)$ máme počáteční podmínky ve tvaru $q(0) = 0$, $q'(0)=I_{ch}(0)=0$.
Převedení soustavy na použitelný tvar vhodný pro aplikaci příslušné numerické metody¶
Jak již bylo řečeno v předchozích úvahách, tak daná soustava diferenciálních rovnic je navzájem neznámými funkcemi propojena což má za následek, že nelze klasickým způsobem soustavu převést na nižší řád.
V ideálním případě lze nalézt tvz. Kanonický tvar diferenciální rovnice. V našem případě by kanonický tvar byl tvořen diferenciální rovnicí druhého řádu a příslušný kanonický tvar by vypadal $y'' = f(x,y,y')$. Pokud takový kanonický tvar lze najít, tak danou rovnici lze pomocí jednoduché substituce:
\begin{equation} y=w_1,~~~\frac{dy}{dt}=\frac{dw_1}{dt}=w_2,~~~\frac{d^2 y}{dt^2}=\frac{d w_2}{dt}, \end{equation}převést na dvě rovnice prvního řádu ve tvaru:
\begin{equation} \frac{d}{dx} \begin{pmatrix} w_1(x) \\ w_2(x) \end{pmatrix} = \begin{pmatrix} w_2 \\ f(x,w_1,w_2) \end{pmatrix}. \end{equation}Touto jednoduchou redukcí na systém diferenciálních rovnic prvního řádu lze systém řešit běžnými numerickými metodami pro řešení obyčejných diferenciálních rovnic. Mezi nejznámější patří Eulerova nebo Runge-Kuttovy metody.
Bohužel v našem případě alespoň prozatím tuto redukci nelze provést kvůli již zmíněné provázanosti, tj. hledané funkce $Q(t)$ a $q(t)$ vystupují v obou rovnicích společně. Proto nelze najít kanonický tvar a bude potřeba danou soustavu ještě upravit.
Tento problém lze vyřešit vhodným zavedením regulární transformace, která danou soustavu eliminuje od zmiňovaného nedostatku. Po provedení příslušných výpočtů potřebných pro nalezení dané transformace jsme dostali:
\begin{equation} W \equiv Q - \frac{M}{L_1} q = Q - K q \end{equation}\begin{equation} w \equiv Q - \frac{L_{ch}}{M} q = Q - J q, \end{equation}kde jsme označili $K = \frac{M}{L_1}$ a $J= \frac{L_{ch}}{M}$.
K této regulární transformaci potřebujeme i její inverzní zpětnou transformaci, kterou dosadíme do naší soustavy. Zpětná transformace je ve tvaru:
\begin{equation} Q= \frac{K w - J W}{K - J},~~~ q= \frac{w-W}{K-J}. \end{equation}Po provedení námi zvolené transformace a příslušném dosazení dostaneme rovnice ve tvaru:
\begin{equation} \frac{d^2 W}{dt^2} = \frac{R_1}{L_1} \frac{L_1 L_{ch}}{M^2 - L_1 L_{ch}} \frac{dW}{dt}- \frac{R_1}{L_1} \frac{M^2}{M^2 - L_1 L_{ch}} \frac{dw}{dt} + \frac{1}{L_1 C} \frac{L_1 L_{ch}}{M^2 - L_1 L_{ch}}W - \frac{1}{L_1 C} \frac{M^2}{M^2 - L_1 L_{ch}} w \end{equation}\begin{equation} \frac{d^2 w}{dt^2} = - \frac{R_{ch} L_{1}}{M^2 - L_1 L_{ch}} \frac{dW}{dt} + \frac{R_{ch} L_{1}}{M^2 - L_1 L_{ch}} \frac{dw}{dt}. \end{equation}Tento tvar už lze snadno převést na požadovaný tvar vhodný pro aplikaci příslušné numerické metody.
Aplikace Numerického řešení na upravenou soustavu¶
Vzniklou soustavu z minulého kroku jsme nyní už schopni převést na soustavu obyčejných diferenciálních rovnic zavedením následující substituce:
\begin{equation} \Omega_1=W,~~~\Omega_2=\frac{d\Omega_1}{dt}=\frac{dW}{dt},~~~\Omega_3=w,~~~\Omega_4=\frac{d\Omega_3}{dt}=\frac{dw}{dt}. \end{equation}Po aplikaci této substituce dostaneme následující soustavu čtyřech diferenciálních rovnic prvního řádu:
\begin{equation} \frac{d\Omega_1}{dt}=\Omega_2 \end{equation}\begin{equation} \frac{d\Omega_2}{dt}= \frac{1}{L_1 C} \frac{L_1 L_{ch}}{M^2 - L_1 L_{ch}} \Omega_1 + \frac{R_1}{L_1} \frac{L_1 L_{ch}}{M^2 - L_1 L_{ch}} \Omega_2 - \frac{1}{L_1 C} \frac{M2}{M2 - L_1 L_{ch}} \Omega_3 - \frac{R_1}{L_1} \frac{M2}{M2 - L_1 L_{ch}} \Omega_4 \end{equation}\begin{equation} \frac{d\Omega_3}{dt}=\Omega_4 \end{equation}\begin{equation} \frac{d\Omega_4}{dt}= - \frac{L_1 R_{ch}}{M^2 - L_1 L_{ch}} \Omega_2 + \frac{L_1 R_{ch}}{M^2 - L_1 L_{ch}} \Omega_4 \end{equation}Tento tvar nevypadá uplně přehledně, ale lze ho zapsat v poněkud přehlednější maticové formě:
\begin{equation} \frac{d}{dt} \begin{pmatrix} \Omega_1(t) \\ \Omega_2(t) \\ \Omega_3(t) \\ \Omega_4(t) \end{pmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0 \\ \frac{1}{L_1 C} \frac{L_1 L_{ch}}{M^2 - L_1 L_{ch}} & \frac{R_1}{L_1} \frac{L_1 L_{ch}}{M^2 - L_1 L_{ch}} & - \frac{1}{L_1 C} \frac{M2}{M2 - L_1 L_{ch}} & - \frac{R_1}{L_1} \frac{M2}{M2 - L_1 L_{ch}} \\ 0 & 0 & 0 & 1 \\ 0 & - \frac{L_1 R_{ch}}{M^2 - L_1 L_{ch}} & 0 & \frac{L_1 R_{ch}}{M^2 - L_1 L_{ch}} \end{bmatrix} \begin{pmatrix} \Omega_1(t) \\ \Omega_2(t) \\ \Omega_3(t) \\ \Omega_4(t) \end{pmatrix}. \end{equation}Z matematiky víme, že pokud bychom byli schopni nalézt vlastní čísla a vlastní vektory této matice, tak by byla možnost nalézt i analytické řešení. Po krátkém zvážení nám ale dojde, že vzhledem k tvaru matice by výsledné analytické řešení bylo velmi komplikované a ne příliž použitelné. Co se ale týče numerického řešení, tak to bude už velmi snadno řešitelné, protože daná soustava je již převedena na požadovaný tvar a nyní zbývá už jen zvolit konkrétní numerickou metodu pro řešení této soustavy.
Nejdříve je však ještě nutné zapsat počáteční podmínky v řeči nových proměnných ve tvaru:
\begin{equation} \vec{\Omega(0)}= \begin{pmatrix} \Omega_1(0) \\ \Omega_2(0) \\ \Omega_3(0) \\ \Omega_4(0) \end{pmatrix} = \begin{pmatrix} Q(0)- K q(0) \\ I_1(0) - K I_{ch}(0) \\ Q(0)- J q(0) \\ I_1(0) - J I_{ch}(0) \end{pmatrix}= \begin{pmatrix} C U_C(0) \\ 0 \\ C U_C(0) \\ 0 \end{pmatrix}. \end{equation}Pro řešení této soustavy rovnic jsem použil program Python a konkrétně pro řešení této soustavy jsem využil knihovny Odeint a tak nalezl konkrétní tvary řešení pro $\vec{\Omega(0)}$.
Nyní už zbývá pouze danou soustavu převést zpět do původních proměnných $Q(t)$ a $q(t)$ a to za pomoci již připravené zpětné transformace souřadnic:
\begin{equation} W = \Omega_1 = Q - K q,~~~ K=\frac{M}{L_1} \end{equation}\begin{equation} w = \Omega_3 = Q - J q,~~~ J=\frac{L_{ch}}{M} \end{equation}\begin{equation} Q = \frac{K \Omega_3 - J \Omega_1}{K-J},~~~q = \frac{ \Omega_3 - \Omega_1}{K-J}. \end{equation}Po aplikaci zpětné transformace v předchozím kroku už zbývá pouze zapsat výsledné tvary řešení našich hledaných fyzikálních funkcí z původní formulace tvorby soustavy z Kirchhoffových zákonů a za použití příslušných fyzikálních zavedení daných veličin. Konkrétně výslednou funkci vybíjení kondenzátoru $U_{C}(t)$, proud protékající tímto primárním obvodem $I_{1}(t)$ a nakonec indukovaný proud protékající sekundárním obvodem $I_{ch}(t)$. Výsledná řešení jsou ve tvaru:
\begin{equation} U_C(t) = \frac{Q(t)}{C} = \frac{1}{C} \frac{K}{K-J} \Omega_3(t) - \frac{1}{C} \frac{J}{K-J} \Omega_1(t) = \frac{1}{C} \frac{M^2}{M^2-L_1 L_{ch}} \Omega_3(t) - \frac{1}{C} \frac{L_1 L_{ch}}{M^2-L_1 L_{ch}} \Omega_1(t) \end{equation}\begin{equation} I_1(t) = \frac{dQ}{dt} = \frac{K}{K-J} \Omega_4(t) - \frac{J}{K-J} \Omega_2(t) = \frac{M^2}{M^2-L_1 L_{ch}} \Omega_4(t) - \frac{L_1 L_{ch}}{M^2-L_1 L_{ch}} \Omega_2(t) \end{equation}\begin{equation} I_{ch}(t) = \frac{dq}{dt} = \frac{1}{K-J} \Omega_4(t) - \frac{1}{K-J} \Omega_2(t) = \frac{M L_1}{M^2-L_1 L_{ch}} \Omega_4(t) - \frac{M L_1}{M^2-L_1 L_{ch}} \Omega_2(t) \end{equation}Nyní se zaměříme na implementaci řešení do pythonu pro parametry tokamaku Golem.