Revision 82dd582045b2ec890b46e78d5419389be4916146 (click the page title to view the current version)
Rogowski Coil
Introduction
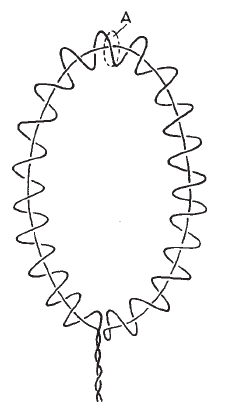
Rogowski coil is an electrical device used for contactless measurement of flowing current. It is a solenoidal coil whose ends are brought around together to form a torus. The whole assembly is then wrapped around a straight conductor. Its voltage output is proportional to the rate of change of current in the conductor.
The advantage of a Rogowski coil over other types of induction coils is that it can be made open-ended and flexible, allowing it to be wrapped round a live conductor being measured without disturbing it.
|
Theory
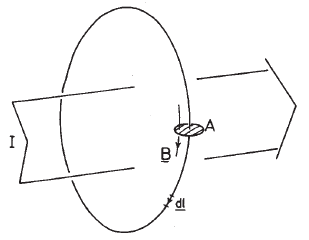
Consider a coil of the uniform cross-sectional area \(A\), with constant turns per unit length - \(n\). Provided the magnetic field varies little over one turn spacing. That is, if
\[ |\nabla B|/B \ll n ,\]
the total flux linkage by the coil \(\Phi\) can be written as an integral rather than a sum over individual turns:
\[ \Phi = n\oint_l dl \oint_A dA\ B \]
where \(dl\) is the line element along the solenoidal axis as illustrated in this figure
|
Note that it is important to have the return wire back down the coil as shown in figure. Otherwise, eqution for \(\Phi\) also includes a term arising from the flux passing through the torus center.
Using Amper’s law :
\[\oint_l B\ dl = \mu I\]
where \(I\) is the total current encircled by \(l\) and \(\mu\) is the magnetic permeability of the medium in the solenoid, the magnetic flux through the Rogowski coil can be written as:
\[ \Phi = nA\mu I \]
The output voltage from the Roqowski coil is
\[ V = \dot{\Phi} = nA\mu\dot{I} \]
It is seen, that the output voltage from the Rogowski coil is directly proportional to the time derivative of total current flowing through its cross-section. Note that it is independent of the distribution of the flowing current.
Credit: Excerpt from
- I. Ďuran: Fluctuations of magnetic field in the CASTOR tokamak, Dissertation Thesis, 2003.
- J. Sentkerestiová: Systematic measurements of plasma position on CASTOR tokamak using magnetic coils and Hall sensors, Diploma Thesis, 2006
Links
- Measuring of the plasma current