Introduction

The determination of the plasma position is one of the basic tasks during the tokamak operation. Plasma tends to expand in the direction of the major radius and further move in the influence of various electric and magnetic fields, which are created during the discharge.

Diagnostic system using for plasma position determination

The Mirnov coils are used for the determiantion of the plasma position on GOLEM. The system consists of 4 magnetic coils placed inside the chamber in the distance of 93 cm from the minor axis. The effective area of the each coil is \(3.8\cdot10^{-3}\) m.

The coils measure the change of the poloidal magnetic field. Ideally, their axis are perpendicular to the toroidal magnetic field, but actually they are slightly deflect and measure the toroidal field too.

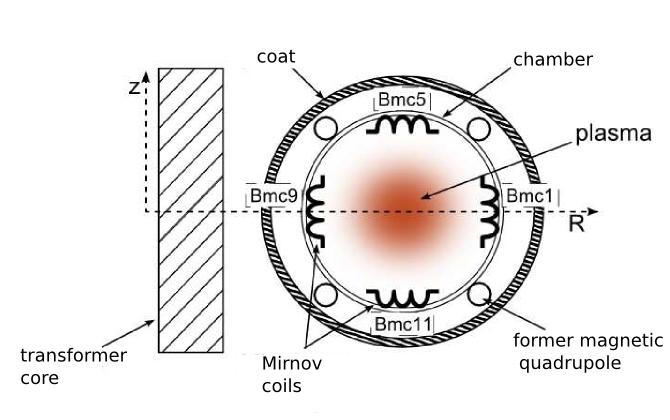
Poloidal cross-section of the tokamak with the places of the Mirnov coils

The straight conductor approximation

It is impossible to express the magnetic field analytically because the plasma is curved to the torus. Therefore we have to make some approximation. Assume an infinite long straight plasma column. From Ampere’s law (\(\nabla\times\mathbf{B}=\mu_0\mathbf{j}\)) flows, that the generated poloidal magnetic field decreases with distance as \(1/r\) from the column’s axis. If we measure the poloidal field on the two opposite sides of the column, its displacement can be expressed as \[\Delta=\frac{B_{\theta=0}-B_{\theta=\pi}}{B_{\theta=0}+B_{\theta=\pi}}\cdot b\] where \(2b\) is the distance between the measuring places (see Fig. 2). This approximation is simple but very rough and is very inaccurate.

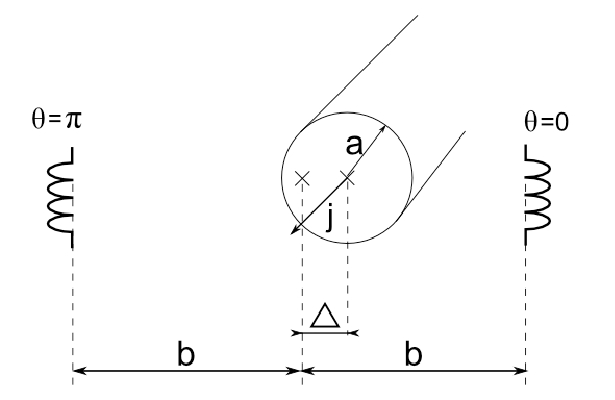
Scheme of the poloidal field measurement for the plasma position determiantion (approximation of the straight conudctor)

Approximation of the large aspect

This approximation is valid only for the tokamak with large aspect, low-\(\beta\) and circular cross-section. The derivation is a little bit more complicated and it is not neccesary to know it for our purposes. For those, who are interested, I recommend

• J. Wesson: Tokamaks, Third edition, Oxford University Press, Clarendon Press, Oxford, 2004 (pages 108 – 120)

• J. P. Freidberg: Ideal Magnetohydrodynamics, Plenum Press, New York 1987 (pages 108 – 122)

• V.S. Mukhovatov, V.D. Shafranov: Plasma Equilibrium in a Tokamak, Nuclear Fusion 11, 605 (1971) (the best of them)

The vertical (\(\Delta_z\)) and horizontal (\(\Delta_R\)) displacement can be expressed as \[\Lambda = \left(\frac{B_1}{2}-\bar{B}_z\right)\frac{R_0}{B_0b}-\ln\frac{b}{a}+1\]

\[\Delta_R = \frac{B_1}{2B_0}b-\frac{1}{2}\left[\ln\frac{a}{b}-1+\left(\Lambda-1/2\right)\left(1+\frac{a^2}{b^2}\right)\right]\frac{b^2}{R_0}\]

\[\Delta_z = \frac{B_2}{2B_0}b\]

\[a = a_L-\sqrt{\Delta_R^2+\Delta_z^2}\]

where

\[B_1=B_\theta(b,\pi)-B_\theta(b,0)\]

\[B_2=B_\theta(b,3\pi/2)-B_\theta(b,\pi/2)\]

\[B_0=\frac{\mu_0I_p}{2\pi b}\] \(a_L\) is the diameter of the limiter, \(b\) is the distance between the center of the minor axis and the measuring place, \(I_p\) is the plasma current, \(\bar{B}_z\) is the average vertical field along the torus and \(\Lambda\) is called "Shafranov excentricity factor".